Technology Deep Dive: Building a Faster ORAM Layer for Enclaves

Private doesn’t mean lonely. Signal’s mission is to help you connect with people in a secure way. This means that you need to know which of your contacts are also on Signal. This is called “contact discovery” and it’s an essential part of any messaging app.

Most other communications apps enable contact discovery by maintaining their own internal social graph or by uploading and storing your full address book on their servers. But Signal enables you to find and connect with people in a privacy-preserving way. In short, we let you see which of your friends use Signal, but we don’t want to know who your friends are. Letting you know which of your contacts are using Signal while preserving the privacy of your social map requires some complex engineering choices on our end.

In this post, we’ll be diving into some new ways that improve our ability to handle contacts in a private way. That’s right folks. We’re getting technical. We’re talking enclaves and memory access patterns. [If you’ve never heard of an enclave before, don’t worry. We’ll explain it soon.]

Our new method is faster and more efficient. It lays the groundwork for the introduction of usernames and phone number privacy which will offer new privacy controls around your phone number’s visibility on Signal.

Our latest development in our use of enclaves has been the implementation of a path-based oblivious RAM (Path ORAM) layer as an improvement over our previous linear scanning methods. Both Path ORAM and linear scanning allow us to let users discover contacts without Signal, or anyone but the user, knowing who these contacts are. But Path ORAM is faster, saves on processing power, and is much more conducive to us building efficient services on top of it.

In the rest of this post, we’ll share how we use enclaves, explain the importance of ORAM as a technique that enables us to make use of those enclaves, explain why a Path ORAM layer is an improvement over our previous methods, and describe its implications for further developments within Signal.

We’ve previously discussed our methods of contact discovery as well as our method of securely storing/verifying recovery keys. So if you’d like some more background on what we’re building on, and how we’ve thought about these questions in the past, we recommend reading these posts before jumping in here.

Enclaves and their uses

Signal uses enclaves for contact discovery. Enclaves isolate data and its processing from everything else going on in a given server, obfuscating it even from server owners/administrators. This means that neither Signal nor the people who run the servers we rely on have access to or knowledge about what’s happening in an enclave. Our use of enclaves allows users to connect via their contacts while preventing Signal’s server owners from extracting the contact lists.

When we talk about enclaves and what they can do for us on the server side at Signal, we’re really discussing two specific capabilities.

First, our enclaves provide remote attestation. Remote attestation is a mechanism by which Signal apps can talk to a server across a network and verify not just that they’re talking to a Signal server (the goal of transport-layer security) but also the exact application logic they’re communicating with. In other words, while TLS verifies who you’re talking to, remote attestations verifies what that other party is doing with the information you’re providing.

Secondly, enclaves protect against introspection. Generally, while running a program on a server, the server’s owner or administrator is able to “introspect” or see the inner workings of that program. They can open up the hood and watch all the requests coming in, the computations being done, and the responses coming out. This is possible because, as owners of the server, administrators can view the raw memory used by a program as it’s running as well as modify all the requests, responses, logic, and states within that memory. Enclaves create a “black box” on the server, a container where something can safely run without being seen.

The enclave solution we use currently on our cloud servers is a technology called SGX built into Intel server processors. Intel’s SGX protects against introspection by encrypting RAM as it’s written into memory and decrypting it as it’s read out. Keys associated with this encryption never leave the underlying CPU, so they’re not accessible to the server owners or anyone else with access to server infrastructure. Someone with access to read the memory space of the program could not access the data because it’s encrypted, and they don’t have the keys to decrypt it. And in Signal’s case, we don’t have these keys either.

Encrypted RAM is a start, but it doesn’t do the full job. Simply knowing how memory is accessed can be enough to leak information. So, when we use enclaves, we build additional protections to defend against information leakage. We use “oblivious RAM” algorithms which work to obscure memory patterns and obfuscate data in enclaves.

Why we need oblivious RAM

To show why oblivious RAM (ORAM) is necessary, we’ll look at a real-life example that demonstrates how memory patterns function in enclaves.

All the phone numbers in the United States can be listed as some subset of numbers from 000-000-0000 to 999-999-9999. A Signal user might want to know if one of their friends, whose phone number they have, is in that list.

A simple way of programming this “find if a number is in a set of numbers” request could be to write out all the numbers, sorted in memory and then use a binary search to find the requested contact within them. In this scenario we’d first check if the number being sought is greater or less than the middle number in our set. If it is greater, we can ignore all numbers smaller than that and recursively look for the number among the top half of our set. If it’s smaller, we can ignore the top half and just look at the bottom. This simple method allows us to find a requested number quickly and easily. Given 1 billion numbers to look through, we can generally find our solution in 30 or so steps.

This solution certainly works. But it also poses some problems. Let’s consider how predictably this program accesses memory–it always jumps into the center of a large array of numbers, then jumps either forward or backward, then jumps again, then again, each jump smaller than the last. Even though those numbers are encrypted, it’s still possible to gather information on which number was looked up.

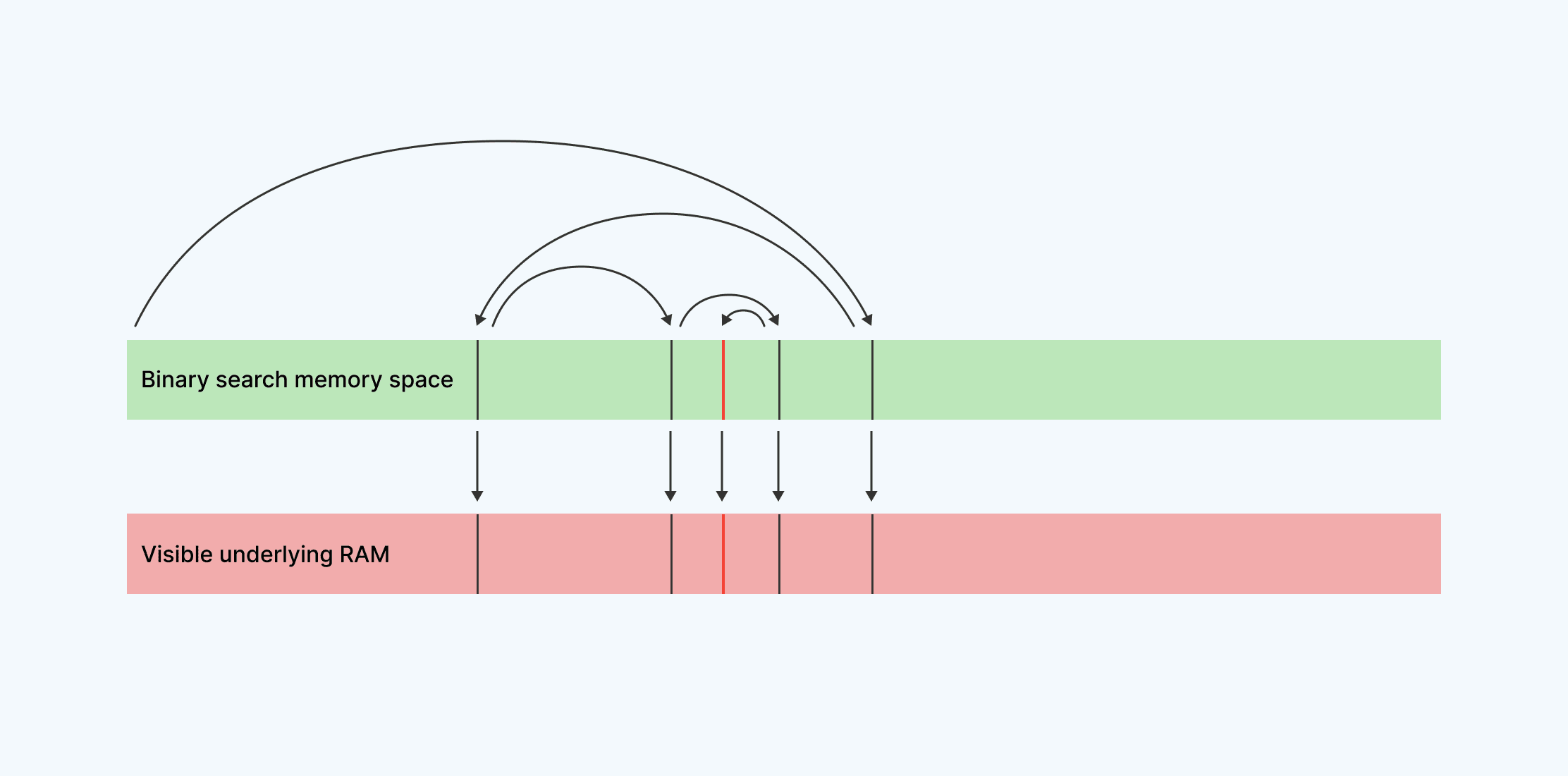
An attacker with system-level administrative privileges to be able to watch RAM access patterns knows the original list of numbers, and they know the path that the program took to look up the number. They know the numbers are sorted. Given this information, they can take those same numbers, sort them again, and with a high degree of confidence find the number they’re looking for (the red line in the above diagram). Because they know where the number was, and where it was is determined by what it was, they can observe information that could help them determine what the number is.

To defend against this type of data leakage, we build algorithms on top of enclaves that obfuscate memory access patterns to prevent this type of information leak. In other words, our patterns of RAM usage aim to be oblivious to their inputs.

One solution: linear scanning

Our previous strategy for protecting against potential information leakage in enclaves has been a linear scanning ORAM method. Here’s how it works: Let’s say we again want to find a number within a list, but this time, rather than a binary search, we just read every number.

We start reading from the beginning, and we don’t stop when we find our number; we keep going all the way through the whole list. The important trait here is that, whether we find the number or not, and wherever the number is within our set, we always follow the same read pattern: start at the beginning, end at the end. This doesn’t leak information, but it’s very slow. Again, considering 1 billion numbers, our binary search in the previous section took 30 comparisons to find the number in question. Linear scanning takes 1 billion. That’s a lot of time and a lot of processing power.

Linear scanning accomplishes the narrow task of obscuring memory access patterns, but it doesn’t do so efficiently or scalably. As we add features (like usernames), we need an approach that can support increased use. We also need to be able to meet the needs of a growing user base. At Signal, this means ensuring we are there to support spikes in usage due to unpredictable global events–the very moments people often rely on us most.

Using a lot of processing power has a real-life cost. Especially in an enclave, CPU-time means dollars. Doing something in 1 billion steps rather than 30 is like paying for gas to drive all the way around the world just to end up a block away from your home. It’s also expensive to take the long way around. As a nonprofit, we depend on donations from our community; we want to make every dollar count.

Further, because linear scans are so slow, they necessarily increase the complexity of the programs that rely on them. If you can’t do one basic thing quickly (look up a number), you’re forced to find clever ways to batch requests, parallel-process work, and otherwise try to regain the time you’ve lost to that slow process.

All this to say, we needed to figure out a better way to manage contact discovery.

Building a better ORAM

So, here’s what’s new.

Rather than tread this path towards ever-increasing program complexity as we try to hand-craft obfuscation into our memory access patterns through linear scanning, we’ve built a layer of abstraction around RAM access that utilizes higher-performing oblivious RAM (ORAM) techniques. We are inspired by the systems discussed in current academic literature, such as Path ORAM, Oblix, and Snoopy and grateful to the researchers who developed and shared them. These techniques take the simplest RAM abstraction of GetDataAtAddress(addr) and SetDataAtAddress(addr, value) and implement them in such a way that access patterns are obfuscated. Here’s how a binary search would look using ORAM:

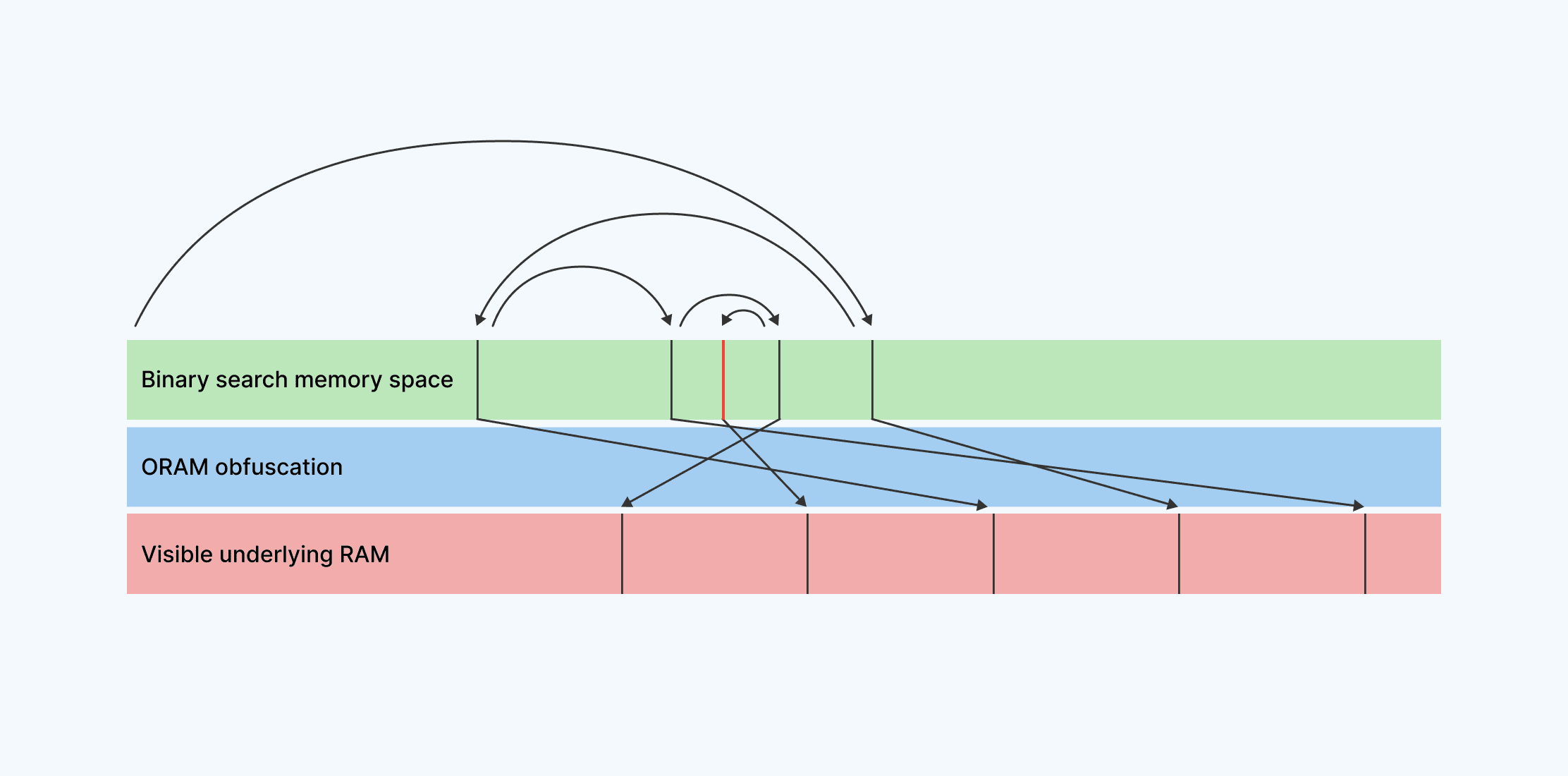
Our new Path ORAM approach obfuscates the locations of our accessed memory. When memory is accessed within a given memory space (for example, the space that contains our list of numbers), the locations of actual reads and writes are mapped to random, ever-changing locations within actual, externally-visible RAM. This allows a high level algorithm, like a binary search, to run normally, while its access patterns are obfuscated and provide no meaningful information to anyone observing them.

Using this method, it would be extremely difficult for an attacker to understand which number is being queried in a given search, even though the number lookup is being done by a known binary-search access pattern.

Let’s take another example to see how an ORAM layer protects against information leaks. Let’s say there is an attacker (with system-level administrative privileges to be able to watch RAM access patterns) who wishes to find which users have a particular number in their contacts. The attacker could approach this problem by looking this number up themselves in the enclave and noting which access pattern (obfuscated by ORAM or no) this lookup caused. They could then look for this same access pattern in all subsequent requests. To handle this potential threat, our implementation of ORAM has another important property: the same lookup done twice will not produce the same pattern. When a subsequent client reads the same contact, they’ll read it with an entirely new memory access pattern.

The position of information is not only randomized, it moves every time it is accessed.

Path ORAM

If building an ORAM layer is the “what,” Path ORAM is the “how,” the algorithm that implements our memory access pattern obfuscation.

Path ORAM divides RAM into fixed-sized segments, which we call blocks. It stores those blocks within a binary tree, where each node of the tree is capable of storing some small number of blocks. Leaf nodes of the tree have unique position identities, or “leaf identities”: the first leaf has identity L1, the second L2, etc. Path ORAM stores each block on a path between the root node and some leaf ( the block itself could be in the root, in an intermediate node, or in the leaf). It remembers the leaf identifier assigned to each block, and it can find that block again by traversing that root-to-leaf path.

Here’s what it looks like:

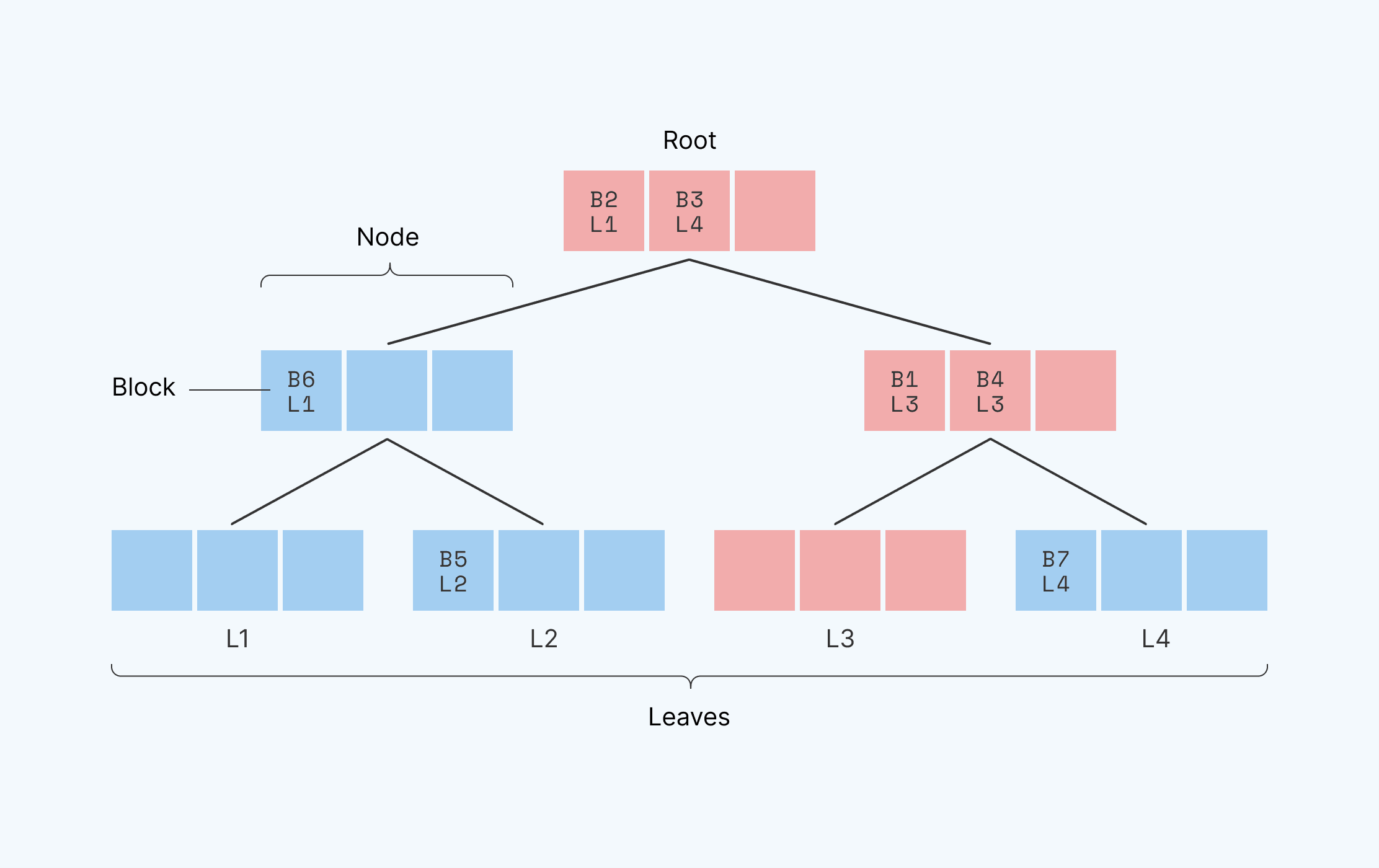
Here, we see a binary tree with three levels and four leaves, with identities L1-L4. Each node in the tree has space for three blocks. In this example, block B1 is mapped to leaf identifier L3. This means that block B1 is along the path between leaf identifier 3 and the route–which we’ve highlighted in red. in one of the red locations–it’s somewhere on the path from the root to leaf L3. [Note that a given block could be along many paths. A block at the root, for example, is along ALL paths. In this case, B1 is technically on the path between the root and both L3 and L4. However, the path that a block is assigned to via its leaf identifier, L3 in this case, is the path that the system recognizes.]

In order to read out the information located in B1, we first read the entire path between L3 and the root (all red blocks) and place this information into a temporary “stash” (a small array). This gives us a smaller data set to search through. We then linearly scan the data in the stash, looking for B1, the block in question, and read/write/utilize its contents. This stash is relatively small, and since we use linear scanning, the memory access pattern is obscured. At this point, we’ve successfully used Path ORAM to locate and read the data in block B1. If we wanted to make changes to a block, we would modify the block in question while it’s still in the stash.

Now, we have to move the data in the stash back into the tree. Before we do so, however, we pick a new location for our block B1. Importantly, our new position must be uniformly random–meaning that our block can with equal probability be assigned any available leaf identifier L1-L4. It used to be at position L3; let’s say it now randomly is slotted at position L4.

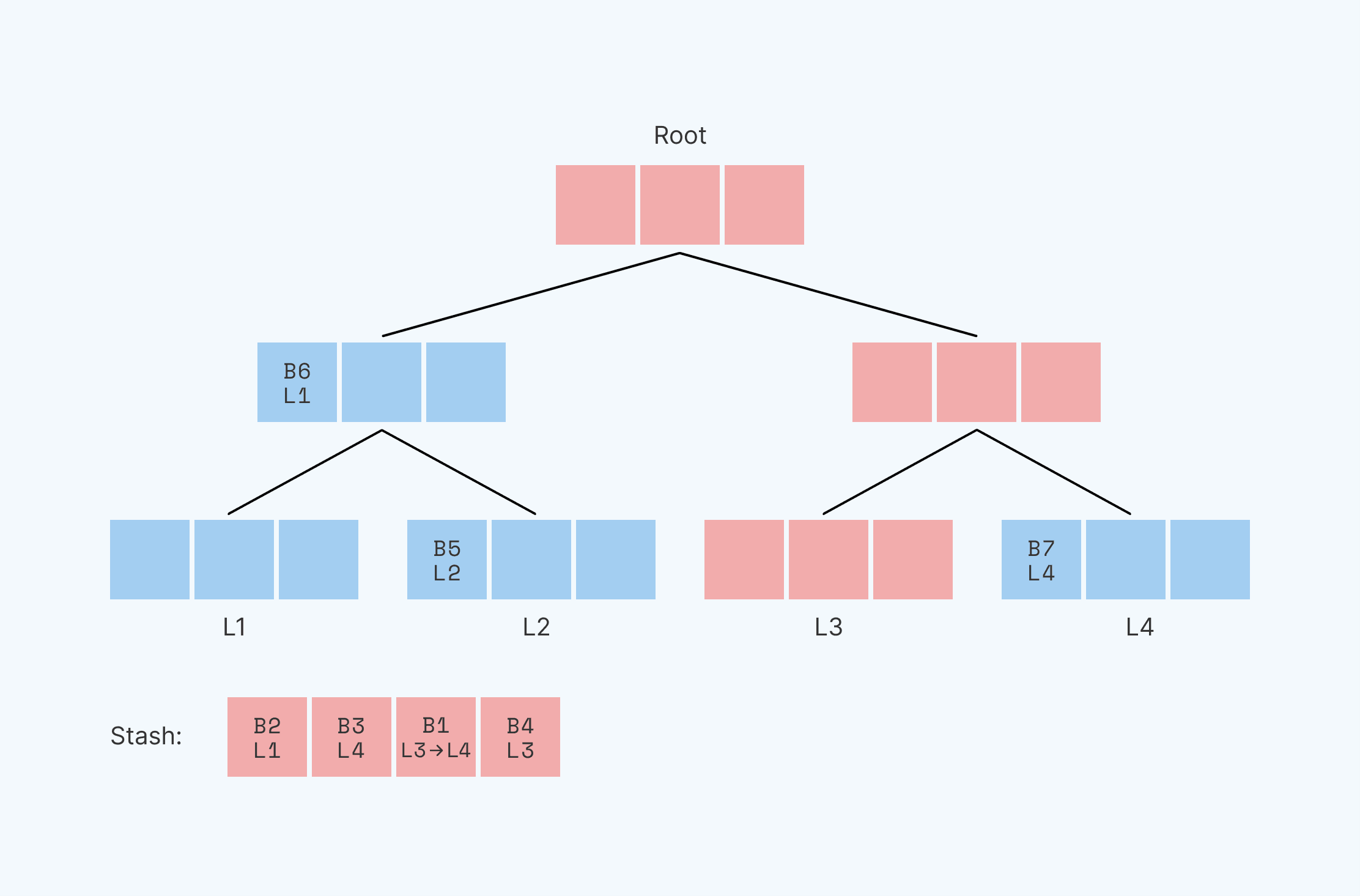
We’ve got a stash that currently contains blocks with positions B2@L1, B3@L4, B1@L4, and B4@L3. We changed the leaf identifier of the block we read, B1, while all others maintain their original leaf identities.

We need to put all of these blocks back in the tree, and we need them to be where Path ORAM can find them the next time we want to read them. Thus, each block must be put on a node that’s somewhere on the path between the root and its leaf identifier. We can’t guarantee that block B4 is going to be put back in the same node or same position that it was before it went into the stash. But we have to ensure that it’s still on the path to its leaf identifier, L3.

To locate and read B1, we read the data along the path from the root to L3, Now we write blocks back starting at L3 and working up to the root. At each node along the way, we see if there are any blocks in the stash that can be written to that node. A block can be written into the node if that node is along the path from the root to that block’s leaf identifier.

In this case, we could write in the blocks as shown here:

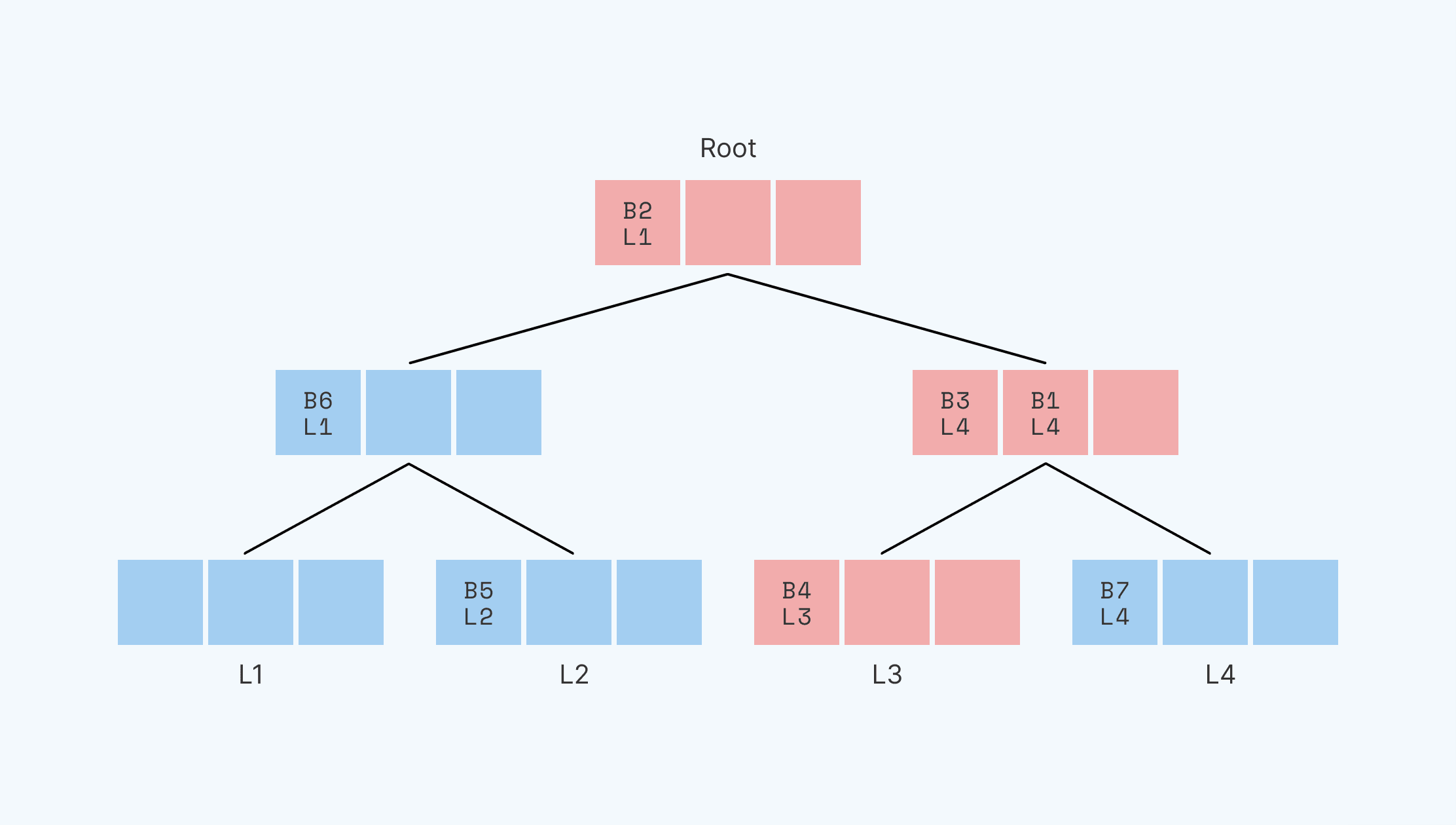
If we had instead chosen to put B1 in L1 or L2 (to label B1 with either of these leaf identities), it would need to be added to the root node, since this is the only node on the L3 path that also intersects with the L1 and L2 paths. If it had reshuffled to the L3 path, B1 would have been located in the L3 leaf along with B4.

So, we iterate the same path twice: once to read into the stash, once to write from the stash back into the tree. Because we iterate the same path in the write, we don’t leak any information about the new position of the block in question.

We do still have one challenge to overcome with this method: sometimes, we may read data into the stash and be unable to return all of it to the tree. Some nodes we want to write to (including the root) may be full. If we’re unable to put a block back in the tree, we keep the block in stash and write it back on some subsequent iteration.

To summarize, when we want to find a block and the data it contains, we:

• Find the block’s current leaf identifier
• Determine the path between the root and the block’s leaf identifier, and proceed along it moving all blocks we find into a stash
• Find the block within the stash using a linear scan method, and either read or modify it
• Pick a new random position for the block
• Proceed back along the path from leaf to root, placing all blocks we can from the stash back into a node along that path

Built for speed

Path ORAM has allowed us to speed up our processing for contact discovery.

In order to support phone number privacy, we need to expand the contact discovery database. Therefore, we will have more data to search for every query. The bigger the dataset, the faster we have to search in order to keep the user experience smooth.

Obviously, the use of Path ORAM slows down each memory access, as each block access requires a path read and a path write, as well as some ancillary processing. But it is far more efficient than relying on linear scanning alone, which had to read all the data in the entire dataset. Moving blocks takes some time, but vastly less, and it results in a faster process overall.

Let’s consider the worst case where each block contains a single contact and each node contains a single block. For 1 billion users, linear scan does 1 billion reads. Using Path ORAM, those 1 billion records are stored in a table with about 2 billion nodes and a depth of about 30 levels. Each block access does 30 reads to pull the entire path from the tree into the stash and find the right block, and 30 writes to put the blocks back into the tree along their path. If we build a binary search algorithm on top of Path ORAM, we expect it to also take ~30 steps to find a contact. So, we’re looking at 30*(30+30)=1800 memory accesses, 1/555555 the number of operations of a linear scan.¹

But it’s not only that Path ORAM processing itself is faster than linear scanning. We can build on top of the Path ORAM layer more easily using simpler, faster code while Path ORAM ensures that the underlying patterns are protected from information leaks. This lets us focus more deeply on implementation, operational efforts, and application logic.

A Path ORAM-enabled future

Now that we’re using Path ORAM to improve the way that we are accessing RAM in our enclaves, what does that mean for the future?

Path ORAM improves our capacity to use enclaves in better, faster ways while maintaining a very high level of security. It will enable us to build other enclave-backed applications going forward. And crucially, it is also flexible enough so that we can continue pushing the field forward as we build new strategies, technologies, and approaches to combine top-level privacy with features and functionalities that our users want and need.

Right now, the implementation of Path ORAM is the backbone for a new era of contact discovery in Signal, one that will let users choose usernames that they could opt to share with people instead of their phone numbers. Usernames have been one of the most requested features throughout Signal’s existence. Making usernames and phone number privacy a reality in Signal is a massive technical undertaking. It’s something we’ve been working on for a long time and will continue to work on for several more months or longer before it’s ready. Implementing Path ORAM for contact discovery is one step on that road, and we’re happy to share this inside look at the foundation we’re laying.

Acknowledgements

Huge thanks to the academic teams behind the publication of the Path ORAM, Oblix, and Snoopy papers. Your open sharing of your ideas has made these technical advances within Signal possible.

Thanks to the engineers that actually put code to paper and made this happen: Rolfe Schmidt, Jon Chambers, Chris Eager, Ravi Khadiwala, Amit Assaf, and me (pats self on back).

Thank you to Meredith Whittaker, Ehren Kret, and Moxie Marlinspike, whose questions and perspectives helped shape this blog post, and to Nina Berman for working tirelessly to wordsmith.

Thank you to the broader cybersecurity community–the professionals, the hackers, the researchers, and the open source enthusiasts. Your diligent testing and probing keeps us collectively safer.