Signal Protocol and Post-Quantum Ratchets

We are excited to announce a significant advancement in the security of the Signal Protocol: the introduction of the Sparse Post Quantum Ratchet (SPQR). This new ratchet enhances the Signal Protocol’s resilience against future quantum computing threats while maintaining our existing security guarantees of forward secrecy and post-compromise security.

The Signal Protocol is a set of cryptographic specifications that provides end-to-end encryption for private communications exchanged daily by billions of people around the world. After its publication in 2013, the open source Signal Protocol was adopted not only by the Signal application but also by other major messaging products. Technical information on the Signal Protocol can be found in the specifications section of our docs site.

In a previous blog post, we announced the first step towards advancing quantum resistance for the Signal Protocol: an upgrade called PQXDH that incorporates quantum-resistent cryptographic secrets when chat sessions are established in order to protect against harvest-now-decrypt-later attacks that could allow current chat sessions to become compromised if a sufficiently powerful quantum computer is developed in the future. However, the Signal Protocol isn’t just about protecting cryptographic material and keys at the beginning of a new chat or phone call; it’s also designed to minimize damage and heal from compromise as that conversation continues.

We refer to these security goals as Forward Secrecy (FS) and Post-Compromise Security (PCS). FS and PCS can be considered mirrors of each other: FS protects past messages against future compromise, while PCS protects future messages from past compromise. Today, we are happy to announce the next step in advancing quantum resistance for the Signal Protocol: an additional regularly advancing post-quantum ratchet called the Sparse Post Quantum Ratchet, or SPQR. On its own, SPQR provides secure messaging that provably achieves these FS and PCS guarantees in a quantum safe manner. We mix the output of this new ratcheting protocol with Signal’s existing Double Ratchet, in a combination we refer to as the Triple Ratchet.

What does this mean for you as a Signal user? First, when it comes to your experience using the app, nothing changes. Second, because of how we’re rolling this out and mixing it in with our existing encryption, eventually all of your conversations will move to this new protocol without you needing to take any action. Third, and most importantly, this protects your communications both now and in the event that cryptographically relevant quantum computers eventually become a reality, and it allows us to maintain our existing security guarantees of forward secrecy and post-compromise security as we proactively prepare for that new world.

The Current State of the Signal Protocol

The original Signal ratchet uses hash functions for FS and a set of elliptic-curve Diffie Hellman (ECDH) secret exchanges for PCS. The hash functions are quantum safe, but elliptic-curve cryptography is not. An example is in order: our favorite users, Alice and Bob, establish a long-term connection and chat over it regularly. During that session’s lifetime, Alice and Bob regularly agree on new ECDH secrets and use them to “ratchet” their session. Mean ol’ Mallory records the entire (encrypted) communication, and really wants to know what Alice and Bob are talking about.

The concept of a “ratchet” is crucial to our current non-quantum FS/PCS protection. In the physical world, a ratchet is a mechanism that allows a gear to rotate forward, but disallows rotation backwards. In the Signal Protocol, it takes on a similar role. When Alice and Bob “ratchet” their session, they replace the set of keys they were using prior with a new set based on both the older secrets and a new one they agree upon. Given access to those new secrets, though, there’s no (non-quantum) way to compute the older secrets. By being “one-way”, this ratcheting mechanism provides FS.

The ECDH mechanism allows Alice and Bob to generate new, small (32 bytes) data blobs and attach them to every message. Whenever each party receives a message from the other, they can locally (and relatively cheaply) use this data blob to agree on a new shared secret, then use that secret to ratchet their side of the protocol. Crucially, ECDH also allows Alice and Bob to both agree on the new secret without sending that secret itself over their session, and in fact without sending anything over the session that Mallory could use to determine it. This description of Diffie-Hellman key exchange provides more details on the concepts of such a key exchange, and this description of ECDH provides specific details on the variant used by the current Signal protocol.

Sometime midway through the lifetime of Alice and Bob’s session, Mallory successfully breaches the defences of both Alice and Bob, gaining access to all of the (current) secrets used for their session at the time of request. Alice and Bob should have the benefits of Forward Secrecy - they’ve ratcheted sometime recently before the compromise, so no messages earlier than their last ratchet are accessible to Mallory, since ratcheting isn’t reversible. They also retain the benefits of Post-Compromise Security. Their ratcheting after Mallory’s secret access agrees upon new keys that can’t be gleaned just from the captured data they pass between each other, re-securing the session.

Should Mallory have access to a quantum computer, though, things aren’t so simple. Because elliptic curve cryptography is not quantum resistant, it’s possible that Mallory could glean access to the secret that Alice and Bob agreed upon, just by looking at the communication between them. Given this, Alice and Bob’s session will never “heal”; Mallory’s access to their network traffic from this point forward will allow her to decrypt all future communications.

Mixing In Quantum Security

In order to make our security guarantees stand up to quantum attacks, we need to mix in secrets generated from quantum secure algorithms. In PQXDH, we did this by performing an additional round of key agreement during the session-initiating handshake, then mixing the resulting shared secret into the initial secret material used to create Signal sessions. To handle FS and PCS, we need to do continuous key agreement, where over the lifetime of a session we keep generating new shared secrets and mixing those keys into our encryption keys.

Luckily there is a tool designed exactly for this purpose: the quantum-secure Key-Encapsulation Mechanism (KEM). KEMs share similar behavior to the Diffie-Hellman mechanisms we described earlier, where two clients provide each other with information, eventually deciding on a shared secret, without anyone who intercepts their communications being able to access that secret. However, there is one important distinction for KEMs - they require ordered, asymmetric messages to be passed between their clients. In ECDH, both clients send the other some public parameters, and both combine these parameters with their locally held secrets and come up with an identical shared secret. In the standardized ML-KEM key-encapsulation mechanism, though, the initiating client generates a pair of encapsulation key (EK) and decapsulation key (DK) (analogous to a public and private key respectively) and sends the EK. The receiving client receives it, generates a secret, and wraps it into a ciphertext (CT) with that key. The initiating client receives that CT and decapsulates with its previously generated DK. In the end, both clients have access to the new, shared secret, just through slightly different means.

Wanting to integrate this quantum-secure key sharing into Signal, we could take a simple, naive approach for each session. When Alice initiates a session with Bob,

• Alice, with every message she sends, sends an EK
• Bob, with every message he receives, generates a secret and a CT, and sends the CT back
• Alice, on receiving a CT, extracts the secret with her DK and mixes it in

This initially simple-looking approach, though, quickly runs into a number of issues we’ll need to address to make our protocol actually robust. First, encapsulation keys and CTs are large - over 1000 bytes each for ML-KEM 768, compared to the 32 bytes required for ECDH. Second, while this protocol works well when both clients are online, what happens when a client is offline? Or a message is dropped or reordered? Or Alice wants to send 10 messages before Bob wants to send one?

Some of these problems have well-understood solutions, but others have trade-offs that may shine in certain circumstances but fall short in others. Let’s dive in and come to some conclusions.

Who Wants What When

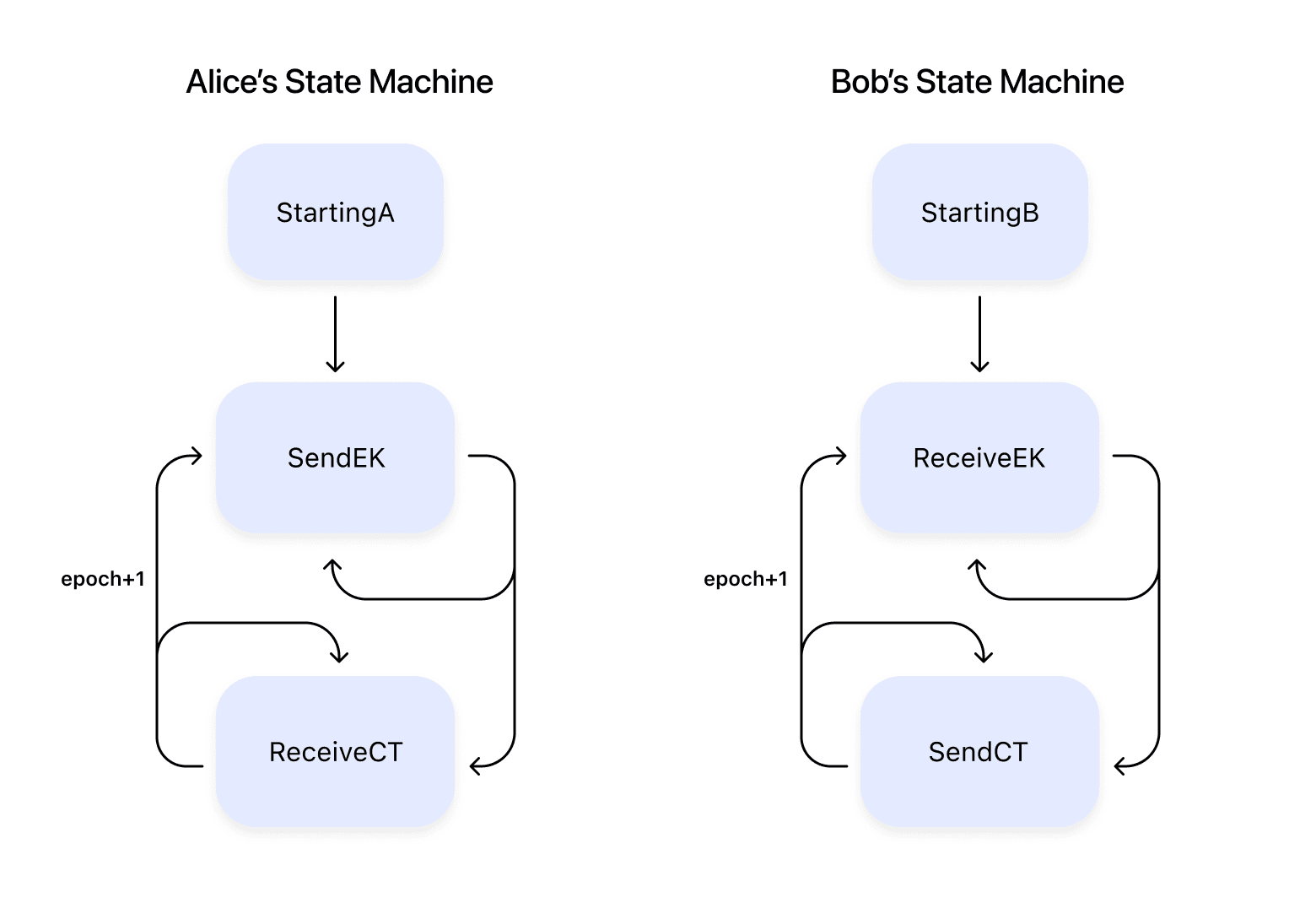
How does Alice decide what to send based on what Bob needs next, and vice versa? If Bob hasn’t received an EK yet, she shouldn’t send the next one. What does Bob send when he hasn’t yet received an EK from Alice, or when he has, but he’s already responded to it? This is a common problem when remote parties send messages to communicate, so there’s a good, well-understood solution: a state machine. Alice and Bob both keep track of “what state am I in”, and base their decisions on that. When sending or receiving a message, they might also change their state. For example:

• Alice wants to send a message, but she’s in a StartingA state, so she doesn’t have an EK. So, she generates an EK/DK pair, stores them locally, and transitions to the SendEK state
• Alice wants to send a message and is in the SendEK state. She sends the EK along with the message
• Alice wants to send another message, but she’s still in the SendEK state. So, she sends the EK with the new message as well
• Bob receives the message with the EK. He generates a secret and uses the EK to create a CT. He transitions to the SendingCT state.
• Bob wants to send a message and he’s in the SendingCT state. He sends the CT along with the message
• Bob wants to send a message and he’s in the SendingCT state. He sends the CT along with the message
• … etc …

By crafting a set of states and transitions, both sides can coordinate what’s sent. Note, though, that even in this simple case, we see problems. For example, we’re sending our (large) EK and (large) CT multiple times.

Say (or Send) Less

We’ve already mentioned that the size of the data we’re sending has increased pretty drastically, from 32 bytes to over 1000 per message. But bandwidth is expensive, especially on consumer devices like client phones, that may be anywhere in the world and have extremely varied costs for sending bytes over the wire. So let’s discuss strategies for conserving that bandwidth.

First, the simplest approach - don’t send a new key with every message. Just, for example, send with every 50 messages, or once a week, or every 50 messages unless you haven’t sent a key in a week, or any other combination of options. All of these approaches tend to work pretty well in online cases, where both sides of a session are communicating in real-time with no message loss. But in cases where one side is offline or loss can occur, they can be problematic. Consider the case of “send a key if you haven’t sent one in a week”. If Bob has been offline for 2 weeks, what does Alice do when she wants to send a message? What happens if we can lose messages, and we lose the one in fifty that contains a new key? Or, what happens if there’s an attacker in the middle that wants to stop us from generating new secrets, and can look for messages that are 1000 bytes larger than the others and drop them, only allowing keyless messages through?

Another method is to chunk up a message. Want to send 1000 bytes? Send 10 chunks of 100 bytes each. Already sent 10 chunks? Resend the first chunk, then the second, etc. This smooths out the total number of bytes sent, keeping individual message sizes small and uniform. And often, loss of messages is handled. If chunk 1 was lost, just wait for it to be resent. But it runs into an issue with message loss - if chunk 99 was lost, the receiver has to wait for all of chunks 1-98 to be resent before it receives the chunk it missed. More importantly, if a malicious middleman wants to stop keys from being decided upon, they could always drop chunk 3, never allowing the full key to pass between the two parties.

We can get around all of these issues using a concept called erasure codes. Erasure codes work by breaking up a larger message into smaller chunks, then sending those along. Let’s consider our 1000 byte message being sent as 100 byte chunks again. After chunk #10 has been sent, the entirety of the original 1000 byte message has been sent along in cleartext. But rather than just send the first chunk over again, erasure codes build up a new chunk #11, and #12, etc. And they build them in such a way that, once the recipient receives any 10 chunks in any order, they’ll be able to reconstruct the original 1000 byte message.

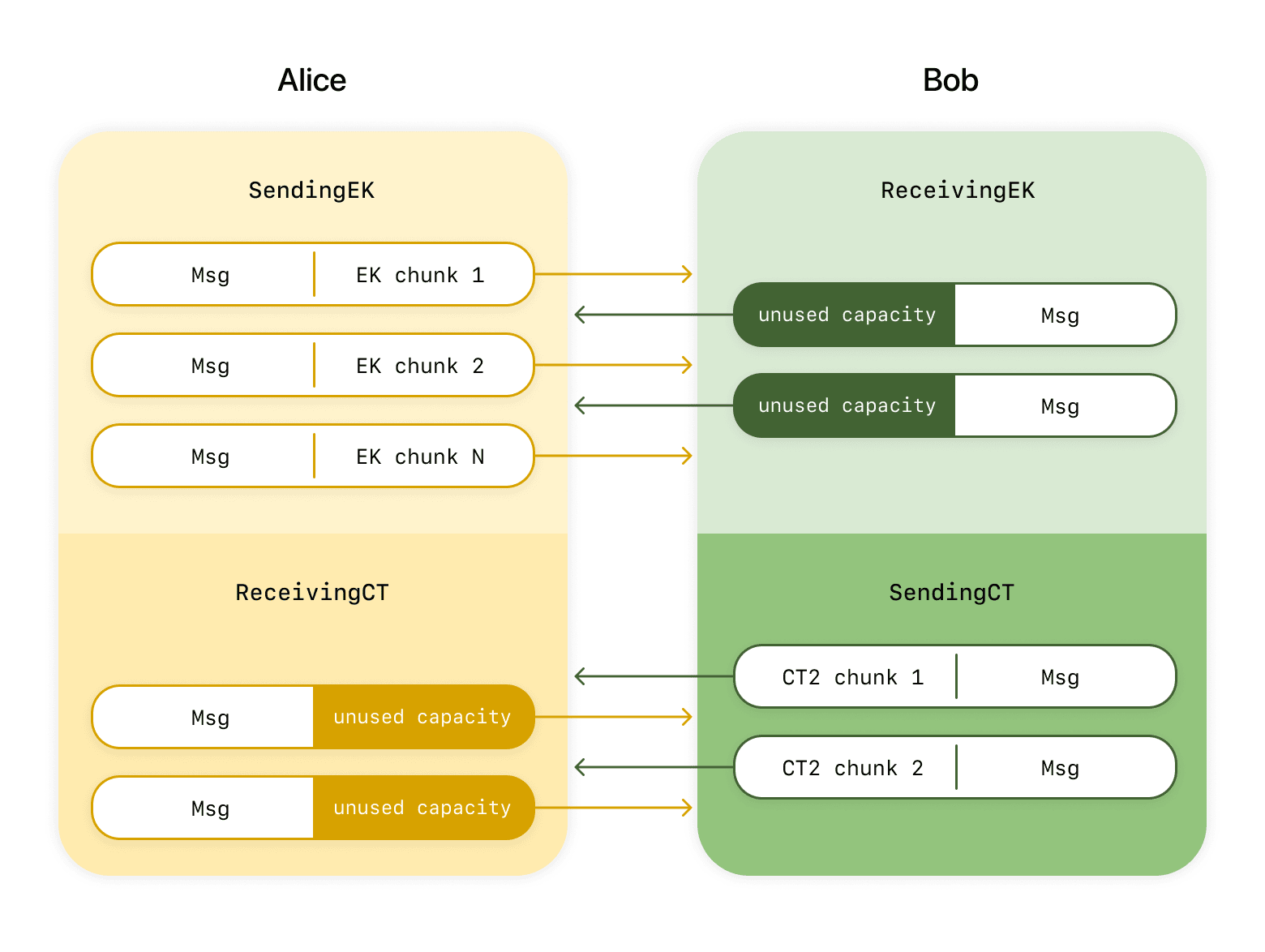
When we put this concept of erasure code chunks together with our previous state machine, it gives us a way to send large blocks of data in small chunks, while handling messages that are dropped. Crucially, this includes messages dropped by a malicious middleman: since any N chunks can be used to recreate the original message, a bad actor would need to drop all messages after #N-1 to disallow the data to go through, forcing them into a complete (and highly noticeable) denial of service. Now, if Alice wants to send an EK to Bob, Alice will:

1. Transition from the StartingA state to the SendingEK state, by generating a new EK and chunking it
2. While in the SendingEK state, send a new chunk of the EK along with any messages she sends
3. When she receives confirmation that the recipient has received the EK (when she receives a chunk of CT), transition to the ReceivingCT state

On Bob’s side, he will:

1. Transition from the StartingB state to the ReceivingEK state when he receives its first EK chunk
2. Keep receiving EK chunks until he has enough to reconstruct the EK
3. At that point, reconstruct the EK, generate the CT, chunk the CT, and transition to the SendingCT state
4. From this point on, he will send a chunk of the CT with every message

One interesting way of looking at this protocol so far is to consider the messages flowing from Alice to Bob as potential capacity for sending data associated with post-quantum ratcheting: each message that we send, we could also send additional data like a chunk of EK or of the CT. If we look at Bob’s side, above, we notice that sometimes he’s using that capacity (IE: in step 4 when he’s sending CT chunks) and sometimes he’s not (if he sends a message to Alice during step 2, he has no additional data to send). This capacity is pretty limited, so using more of it gives us the potential to speed up our protocol and agree on new secrets more frequently.

A Meditation On How Faster Isn’t Always Better

We want to generate shared secrets, then use them to secure messages. So, does that mean that we want to generate shared secrets as fast as possible? Let’s introduce a new term: an epoch. Alice and Bob start their sessions in epoch 0, sending the EKs for epoch 1 (EK#1) and associated ciphertext (CT#1) to each other. Once that process completes, they have a new shared secret they use to enter epoch 1, after which all newly sent messages are protected by the new secret. Each time they generate a new shared secret, they use it to enter a new epoch. Surely, every time we enter a new epoch with a new shared secret, we protect messages before that secret (FS) and after that secret (PCS), so faster generation is better? It seems simple, but there’s an interesting complexity here that deserves attention.

First, let’s discuss how to do things faster. Right now, there’s a lot of capacity we’re not using: Bob sends nothing while Alice sends an EK, and Alice sends nothing while Bob sends a CT. Speeding this up isn’t actually that hard. Let’s change things so that Alice sends EK#1, and once Bob acknowledges its receipt, Alice immediately generates and sends EK#2. And once she notices Bob has received that, she generates and sends EK#3, etc. Whenever Alice sends a new message, she always has data to send along with it (new EK chunks), so she’s using its full capacity. Bob doesn’t always have a new CT to send, but he is receiving EKs as fast as Alice can send them, so he often has a new CT to send along.

But now let’s consider what happens when an attacker gains access to Alice. Let’s say that Alice has sent EK#1 and EK#2 to Bob, and she’s in the process of sending EK#3. Bob has acknowledged receipt of EK#1 and EK#2, but he’s still in the process of sending CT#1, since in this case Bob sends fewer messages to Alice than vice versa. Because Alice has already generated 3 EKs she hasn’t used, Alice needs to keep the associated DK#1, DK#2, and DK#3 around. So, if at this point someone maliciously gains control of Alice’s device, they gain access to both the secrets associated with the current epoch (here, epoch 0) and to the DKs necessary to reconstruct the secrets to other epochs (here, epochs 1, 2, and 3) using only the over-the-wire CT that Bob has yet to send. This is a big problem: by generating secrets early, we’ve actually made the in-progress epochs and any messages that will be sent within them less secure against this single-point-in-time breach.

To test this out, we at Signal built a number of different state machines, each sending different sets of data either in parallel or serially. We then ran these state machines in numerous simulations, varying things like the ratio of messages sent by Alice vs Bob, the amount of data loss or reordering, etc. And while running these simulations, we tracked what epochs’ secrets were exposed at any point in time, assuming an attacker were to breach either Alice’s or Bob’s secret store. The results showed that, in general, while simulations that handled multiple epochs’ secrets in parallel (IE: by sending EK#2 before receipt of CT#1) did generate new epochs more quickly, they actually made more messages vulnerable to a single breach.

But Let’s Still Be Efficient

This still leaves us with a problem, though: the capacity present in messages we send in either direction is still a precious resource, and we want to use it as efficiently as possible. And our simple approach of Alice’s “send EK, receive CT, repeat” and Bob’s “receive EK, send CT, repeat” leaves lots of time where Alice and Bob have nothing to send, should that capacity be available.

To improve our use of our sending capacity, we decided to take a harder look into the ML-KEM algorithm we’re using to share secrets, to see if there was room to improve. Let’s break things down more and share some actual specifics on the ML-KEM algorithm.

1. Alice generates an EK of 1184 bytes to send to Bob, and an associated DK
2. Bob receives the EK
3. Bob samples a new shared secret (32 bytes), which he encrypts with EK into a CT of 1088 bytes to send to Alice
4. Alice receives the CT, uses the DK to decrypt it, and now also has access to the 32 byte shared secret

Diving in further, we can break out step #3 into some sub-steps

1. Alice generates an EK of 1184 bytes to send to Bob, and an associated DK
2. Bob receives the EK
3. Bob samples a new shared secret (32 bytes), which he encrypts with EK into a CT of 1088 bytes to send to Alice¹
   1. Bob creates a new shared secret S and sampled randomness R by sampling entropy and combining it with a hash of EK
   2. Bob hashes the EK into a Hash
   3. Bob pulls 32 bytes of the EK, a Seed
   4. Bob uses the Seed and R to generate the majority of the CT
   5. Bob then uses S and EK to generate the last portion of the CT
4. Alice receives the CT, uses the DK to decrypt it, and now also has access to the 32 byte shared secret

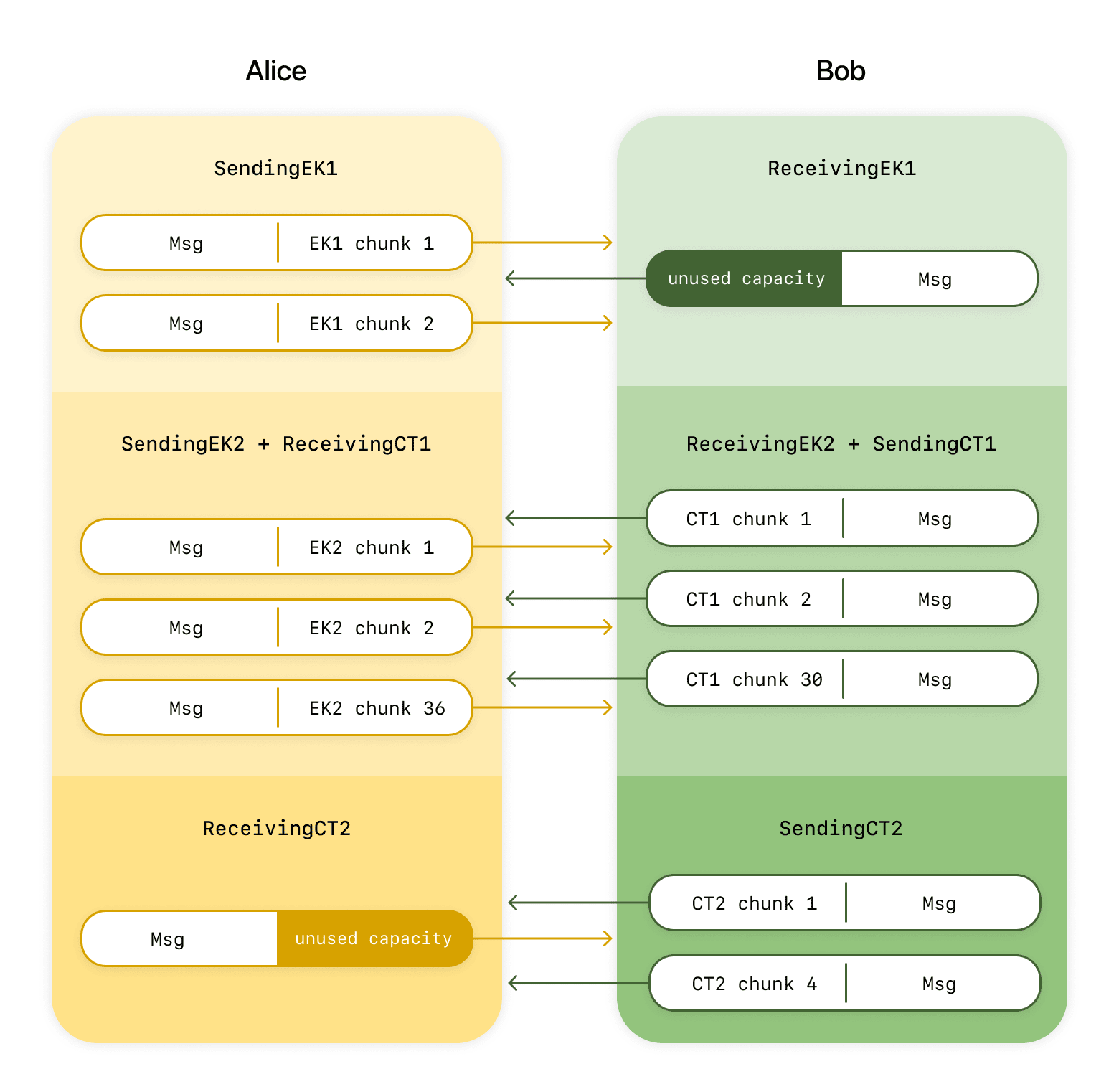
Step 3.d, which generates 960 bytes of the 1088-byte CT, only needs 64 bytes of input: a Seed that’s 32 of EK’s bytes, and the hash of EK, which is an additional 32. If we combine these values and send them first, then most of EK and most of the CT can be sent in parallel from Alice to Bob and Bob to Alice respectively. Our more complicated but more efficient secret sharing now looks like this:

1. Alice generates EK and DK. Alice extracts the 32-byte Seed from EK
2. Alice sends 64 bytes EK₁ (Seed + Hash(EK)) to Bob. Bob sends nothing during this time.
3. Bob receives the Seed and Hash, and generates the first, largest part of the CT from them (CT₁)
4. After this point, Alice sends EK₂ (the rest of the EK minus the Seed), while Bob sends CT₁
5. Bob eventually receives EK₂, and uses it to generate the final portion of the CT (CT₂)
6. Once Alice tells Bob that she has received all of CT₁, Bob sends Alice CT₂. Alice sends nothing during this time.
7. With both sides having all of the pieces of EK and the CT that they need, they extract their shared secret and increment their epoch

There are still places in this algorithm (specifically steps 2 and 6) where one side has nothing to send. But during those times, the other side has only a very small amount of information to send, so the duration of those steps is minimal compared to the rest of the process. Specifically, while the full EK is 37 chunks and the full CT is 34, the two pieces of the new protocol which must be sent without data being received (EK₁ and CT₂) are 2 and 4 chunks respectively, while the pieces that can be sent while also receiving (EK₂ and CT₁) are the bulk of the data, at 36 and 30 chunks respectively. Far more of our sending capacity is actually used with this approach.

Remember that all of this is just to perform a quantum-safe key exchange that gives us a secret we can mix into the bigger protocol. To help us organize our code, our security proofs, and our understanding better we treat this process as a standalone protocol that we call the ML-KEM Braid.

This work was greatly aided by the authors of the libcrux-ml-kem Rust library, who graciously exposed the APIs necessary to work with this incremental version of ML-KEM 768. With this approach completed, we’ve been able to really efficiently use the sending capacity of messages sent between two parties to share secrets as quickly as possible without exposing secrets from multiple epochs to potential attackers.

Mixing Things Up - The Triple Ratchet

There are plenty of details to add to make sure that we reached every corner - check those out in our online protocol documentation - but this basic idea lets us build secure messaging that has post-quantum FS and PCS without using up anyone’s data. We’re not done, though! Remember, at the beginning of this post we said we wanted post-quantum security without taking away our existing guarantees.

While today’s Double Ratchet may not be quantum safe, it provides a high level of security today and we believe it will continue to be strong well into the future. We aren’t going to take that away from our users. So what can we do?

Our answer ends up being really simple: we run both the Double Ratchet and the Sparse Post Quantum Ratchet alongside each other and mix their keys together, into what we’re calling the Triple Ratchet protocol. When you want to send a message you ask both the Double Ratchet and SPQR “What encryption key should I use for the next message?” and they will both give you a key (along with some other data you need to put in a message header). Instead of either key being used directly, both are passed into a Key Derivation Function - a special function that takes random-enough inputs and produces a secure cryptographic key that’s as long as you need. This gives you a new “mixed” key that has hybrid security. An attacker has to break both our elliptic curve and ML-KEM to even be able to distinguish this key from random bits. We use that mixed key to encrypt our message.

Receiving messages is just as easy. We take the message header - remember it has some extra data in it - and send it to the Double Ratchet and SPQR and ask them “What key should I use to decrypt a message with this header?” They both return their keys and you feed them both into that Key Derivation Function to get your decryption key. After that, everything proceeds just like it always has.

Heterogeneous Rollout

So we’ve got this new, snazzy protocol, and we want to roll it out to all of our users across all of their devices… but none of the devices currently support that protocol. We roll it out to Alice, and Alice tries to talk to Bob, but Alice speaks SPQR and Bob doesn’t. Or we roll it out to Bob, but Alice wants to talk to Bob and Alice doesn’t know the new protocol Bob wants to use. How do we make this work?

Let’s talk about the simplest option: allowing downgrades. Alice tries to establish a session with Bob using SPQR and sends a message over it. Bob fails to read the message and establish the session, because Bob hasn’t been upgraded yet. Bob sends Alice an error, so Alice has to try again. This sounds fine, but in practice it’s not tenable. Consider what happens if Alice and Bob aren’t online at the same time… Alice sends a message at 1am, then shuts down. Bob starts up at 3am, sends an error, then shuts down. Alice gets that error when she restarts at 5am, then resends. Bob starts up at 7am and finally gets the message he should have received at 3am, 4 hours behind schedule.

To handle this, we designed the SPQR protocol to allow itself to downgrade to not being used. When Alice sends her first message, she attaches the SPQR data she would need to start up negotiation of the protocol. Noticing that downgrades are allowed for this session, Alice doesn’t mix any SPQR key material into the message yet. Bob ignores that data, because it’s in a location he glosses over, but since there’s no mixed in keys yet, he can still decrypt the message. He sends a response that lacks SPQR data (since he doesn’t yet know how to fill it in), which Alice receives. Alice sees a message without SPQR data, and understands that Bob doesn’t speak SPQR yet. So, she downgrades to not using it for that session, and they happily talk without SPQR protection.

There’s some scary potential problems here… let’s work through them. First off, can a malicious middleman force a downgrade and disallow Alice and Bob from using SPQR, even if both of them are able to? We protect against that by having the SPQR data attached to the message be MAC’d by the message-wide authentication code - a middleman can’t remove it without altering the whole message in such a way that the other party sees it, even if that other party doesn’t speak SPQR. Second, could some error cause messages to accidentally downgrade sometime later in their lifecycle, due either to bugs in the code or malicious activity? Crucially, SPQR only allows a downgrade when it first receives a message from a remote party. So, Bob can only downgrade if he receives his first message from Alice and notices that she doesn’t support SPQR, and Alice will only downgrade if she receives her first reply from Bob and notices that he doesn’t. After that first back-and-forth, SPQR is locked in and used for the remainder of the session.

Finally, those familiar with Signal’s internal workings might note that Signal sessions last a really long time, potentially years. Can we ever say “every session is protected by SPQR”, given that SPQR is only added to new sessions as they’re being initiated? To accomplish this, Signal will eventually (once all clients support the new protocol) roll out a code change that enforces SPQR for all sessions, and that archives all sessions which don’t yet have that protection. After the full rollout of that future update, we’ll be able to confidently assert complete coverage of SPQR.

One nice benefit to setting up this “maybe downgrade if the other side doesn’t support things” approach is that it also sets us up for the future: the same mechanisms that allow us to choose between SPQR or no-SPQR are designed to also allow us to upgrade from SPQR to some far-future (as yet unimagined) SPQRv2.

Making Sure We Get It Right

Complex protocols require extraordinary care. We have to ensure that the new protocol doesn’t lose any of the security guarantees the Double Ratchet gives us. We have to ensure that we actually get the post-quantum protection we’re aiming for. And even then, after we have full confidence in the protocol, we have to make sure that our implementation is correct and robust and stays that way as we maintain it. This is a tall order.

To make sure we got this right, we started by building the protocol on a firm foundation of fundamental research. We built on the years of research the academic community has put into secure messaging and we collaborated with researchers from PQShield, AIST, and NYU to explore what was possible with post-quantum secure messaging. In a paper at Eurocrypt 25 we introduced erasure code based chunking and proposed the high-level Triple Ratchet protocol, proving that it gave us the post-quantum security we wanted without taking away any of the security of the classic Double Ratchet. In a follow up paper at USENIX 25, we observed that there are many different ways to design a post-quantum ratchet protocol and we need to pick the one that protects user messages the best. We introduced and analyzed six different protocols and two stood out: one is essentially SPQR, the other is a protocol using a new KEM, called Katana, that we designed just for ratcheting. That second one is exciting, but we want to stick to standards to start!

Formal Verification From the Start

This research gave us the framework to think about protocol design and prove protocols are secure, but there is a big leap from an academic paper to code. Already when designing PQXDH - a much simpler protocol! - we found that formal verification was an important tool for getting the details right. With the Triple Ratchet we partnered with Cryspen and made formal verification part of the process from the beginning.

As we kept finding better protocol candidates - and we implemented around a dozen of them - we modeled them in ProVerif to prove that they had the security properties we needed. Rather than wrapping up a protocol design and performing formal verification as a last step we made it a core part of the design process. Now that the design is settled, this gives us machine verified proof that our protocol has the security properties we demand from it. We wrote our Rust code to closely match the ProVerif models, so it is easy to check that we’re modeling what we implement. In particular, ProVerif is very good at reasoning about state machines, which we’re already using, making the mapping from code to model much simpler.

We are taking formal verification further than that, though. We are using hax to translate our Rust implementation into F* on every CI run. Once the F* models are extracted, we prove that core parts of our highly optimized implementation are correct, that function pre-conditions and post-conditions cannot be violated, and that the entire crate is panic free. That last one is a big deal. It is great for usability, of course, because nobody wants their app to crash. But it also matters for correctness. We aggressively add assertions about things we believe must be true when the protocol is running correctly - and we crash the app if they are false. With hax and F*, we prove that those assertions will never fail.

Formal Verification Doesn’t Freeze Our Progress

Often when people think about formally verified protocol implementations, they imagine a one-time huge investment in verification that leaves you with a codebase frozen in time. This is not the case here. We re-run formal verification in our CI pipeline every time a developer pushes a change to GitHub. If the proofs fail then the build fails, and the developer needs to fix it. In our experience so far, this is usually as simple as adding a pre- or postcondition or returning an error when a value is out of bounds. For us, formal verification is a dynamic part of the development process and ensures that the quality is high on every merge.

TLDR

Signal is rolling out a new version of the Signal Protocol with the Triple Ratchet. It adds the Sparse Post-Quantum Ratchet, or SPQR, to the existing Double Ratchet to create a new Triple Ratchet which gives our users quantum-safe messaging without taking away any of our existing security promises. It’s being added in such a way that it can be rolled out without disruption. It’s relatively lightweight, not using much additional bandwidth for each message, to keep network costs low for our users. It’s resistant to meddling by malicious middlemen - to disrupt it, all messages after a certain time must be dropped, causing a noticeable denial of service for users. We’re rolling it out slowly and carefully now, but in such a way that we’ll eventually be able to say with confidence “every message sent by Signal is protected by this.” Its code has been formally verified, and will continue to be so even as future updates affect the protocol. It’s the combined effort of Signal employees and external researchers and contributors, and it’s only possible due to the continued work and diligence of the larger crypto community. And as a user of Signal, our biggest hope is that you never even notice or care. Except one day, when headlines scream “OMG, quantum computers are here”, you can look back on this blog post and say “oh, I guess I don’t have to care about that, because it’s already been handled”, as you sip your Nutri-Algae while your self-driving flying car wends its way through the floating tenements of Megapolis Prime.